Demystifying Bayes' Decision Rule
Bayesian decision theory is a fundamental statistical approach to solve classification problems. It relies on prior probabilities and class conditional densities to reach a decision. Often it is stated that Bayes classifier is the most optimum among all classifiers and it has the least error. In simple terms it aims to minimize the probability of error in classification problems.
One should also think that if in fact Bayes’ classifier is the best classifier for any classification problem, why do we need other classification methods in the first place! Also, how do we define “best”? To answer all these questions we need to get a little rigorous and see how Bayes’ theorem is build up from the first principles. It is important to understand these things before blindly applying in my opinion otherwise things can get very nasty in a very short span of time when dealing with complex problems.
Since I don’t wan’t the generalizations to obscure the central points, I will consider a case of only two classes and one feature. Let $\Omega \in \Re^d$ be our sample space which is the set of all possible features in a $d$ dimensional Eucledian space. $d$ is the number of features and in our case $d = 1$. And let that feature be denoted by $x \in \Re$. We are only concerned about two classes as of now, so we partition our space into two sets $\Omega_1$ and $\Omega_2$. Since these two sets are partitions of the sample space they have the following properties:
- $\Omega_1 \cup \Omega_2 = \Omega$
- $\Omega_1 \cap \Omega_2 = \phi$
- $\Omega_1 \ne \phi$ and $\Omega_2 \ne \phi$
We also define a decision $D(\Omega_1, \Omega_2)$:
- $x \in \Omega_1 \Longrightarrow x$ is in class 1
- $x \in \Omega_2 \Longrightarrow x$ is in class 2
It is important to note that the decision $D$ is not symmetric according to our definition. Before things get out of hand lets give some context to our abstractions.
Suppose in a room there are 30% males and 70% females. We have no other information at this point. If we pick a random person from the room there is a 70% chance that it is a female rather than a male. If we want to design a classifier based on this information alone, the most obvious choice would be to always assign the class with higher probability. So far so good, but this classifier will only give us one output, i.e. always classify as a female. So it will be wrong 30% of the times since that is the probability of picking a male.To formalize our discussion lets call the two classes as $\omega_1$ and $\omega_2$. We have information about $P(\omega_1)$ and $P(\omega_2)$. In our case $P(\omega_1) = 0.3$ and $P(\omega_2) = 0.7$. These probabilities of individual classes are also known as prior probabilities. Also, $P(\omega_1) + P(\omega_2) = 1$. A classifier based on this information will always classify a sample in class $\omega_2$. So probability of error in this case is equal to $P(\omega_1)$, since error occurs when our sample is in $\omega_1$, but is classified as $\omega_2$.
If in addition to the class priors we also have the knowledge of class conditional distributions over some variable, we can probably improve our decision. In our case lets say that we also know the probability density function of height for males and for females ($P$(height|male) and $P$(height|female)). Here height becomes our only feature $x$. Class conditional densities are thus represented by $p(x|\omega_1)$ and $p(x|\omega_2)$, i.e, given a class what is probability of observing the feature. (We generally use an upper case $P(\cdot)$ to denote a probability mass function and a lower case $p(\cdot)$ to denote a probability density function).
Let us return to our problem again and we randomly pick a person from the room. But this time we also give the height of the person. How should we classify the person now? The question is how do we use this additional information to design a better classifier. It all boils down to reducing the probability of error. Intutively one can think that what we need is $P(\omega_i|x)$ to make a decision, i.e., the probability of observing male or female given a height. It turns out in fact that this is the best way to deal with the problem. Let’s see how!
We construct what I call an error table -
| $x$ classified as class 1 | $x$ classified as class 2 | |
|---|---|---|
| $x$ actually in class 1 | No Error | $\mathcal{E}_1$ |
| $x$ actually in class 2 | $\mathcal{E}_2$ | No Error |
If $x$ is actually in class 1 and is also classified as class 1 according to our decision rule, then there is no error incurred. Similarly for class 2. But if $x$ is in class 1 but classified as class 2 or vice versa, there is some error.(How many error terms will be there if we have $n$ classes?) We already introduced the partition of our sample space and the decision $D(\Omega_1, \Omega_2)$.
$\mathcal{E}_1$ = probability of error when $x$ is classified as class 2 but is actually in class 1
= probability of error when $x \in \Omega_2$ but is actually in class 1 (decision is incorrect)
= $P(x \in \Omega_2 | \omega_1) P(\omega_1)$
= $P(\omega_1) \int_{\Omega_2} p(x|\omega_1)dx$
There is a more intutive way to think about the probability of error. In the previous case when we had no information about the class conditionals, the probability of error was $P(\omega_1)$ (if $P(\omega_2)>P(\omega_1)$). Now we have more information about our classes and we need to update the probability of error. In the image below two class conditional distributions are shown. Lets say that we have partitioned our domain into $\Omega_1$ and $\Omega_2$ for our decision, i.e. $x \in \Omega_1 \Longrightarrow x \in \omega_1$ and vice versa for class 2.The integration of $p(x|\omega_1)$ over all $x$ which lies in partition $\Omega_2$ gives the probability of error when the sample is classfied as class 2 but is actually in 1.
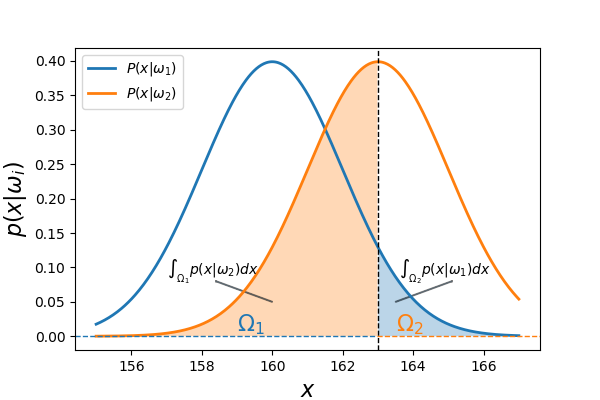
Similarly, $\mathcal{E}_2 = P(\omega_2) \int_{\Omega_1} p(x|\omega_2)dx$. If the definitions of the error terms is clear, then rest is just a trivial calculation. It should also be noted that we are just concerned about the probability of misclassification and not about the cost of misclassification at this point.
Define $\mathcal{E}(\Omega_1, \Omega_2) = \mathcal{E}_1 + \mathcal{E}_2$
Let $\mathcal{D} = { D(\Omega_1, \Omega_2) }$ be the set of all possible decisions. Then our classification problem is reduced to finding $D(\Omega_1^o, \Omega_2^o)$:
$\mathcal{E}(\Omega_1^o, \Omega_2^o) \le \mathcal{E}(\Omega_1,\Omega_2) \forall D(\Omega_1, \Omega_2) \in \mathcal{D}$.
Then $D(\Omega_1^o, \Omega_2^o)$ is the optimal decision rule.
$\mathcal{E}(\Omega_1, \Omega_2) = P(\omega_1) \int_{\Omega_2} p(x|\omega_1)dx + P(\omega_2) \int_{\Omega_1}p(x|\omega_2)dx$
$ = P(\omega_1) \int_{\Omega_2} p(x|\omega_1)dx + P(\omega_2) \int_{\Omega_1} p(x| \omega_2)dx + P(\omega_1) \int_{\Omega_1} p(x|\omega_1)dx - P(\omega_1) \int_{\Omega_1} p(x|\omega_1)dx$
$ = P(\omega_1) \int_{\Omega_1 \cup \Omega_2} p(x|\omega_1)dx + \int_{\Omega_1} P(\omega_2)p(x|\omega_2) - P(\omega_1)p(x|\omega_1)dx$
$ = P(\omega_1) + \int_{\Omega_1} P(\omega_2) p(x|\omega_2) - P(\omega_1) p(x|\omega_1)dx$
Similarly, if we add and subtract $P(\omega_2) \int_{\Omega_2} p(x|\omega_2)dx$ from $\mathcal{E}(\Omega_1,\Omega_2)$, we end up with - $\mathcal{E}(\Omega_1, \Omega_2) = P(\omega_2) + \int_{\Omega_2} P(\omega_1)p(x|\omega_1) - P(\omega_2)p(x|\omega_2)dx$
Adding both errors we get -
$\mathcal{E}(\Omega_1, \Omega_2) = 1 + \int_{\Omega_1} P(\omega_2) p(x|\omega_2) - P(\omega_1) p(x|\omega_1) dx + \int_{\Omega_2} P(\omega_1) p(x|\omega_1) - P(\omega_2) p(x|\omega_2) dx$
A factor of half has no effect on the minimization problem. If we want to minimize this error we need to minimize both the integrals on the right hand side of the equation. If both integrals are integrating over negative quantities, the error achieved will be the minimum.
Let $c_1 = \{x: P(\omega_1)p(x|\omega_1) > P(\omega_2)p(x|\omega_2)\}$
$c_2 = \{ x: P(\omega_1)p(x|\omega_1) = P(\omega_2)p(x|\omega_2)\}$
$c_3 = \{ x: P(\omega_1)p(x|\omega_1) < P(\omega_2)p(x|\omega_2) \}$
Partitioning our sample space again in sets $c_1$, $c_2$ and $c_3$ helps us in making the choice to find the optimum partitions $\Omega_1^o$ and $\Omega_2^o$. To minimize the first integral over the domain $\Omega_1$ we should integrate where $x \in c_1$ and to minimize the integral over the domain $\Omega_2$ we should integrate where $x \in c_3$. This gives us -
$\Omega_1^o = c_1 \cup c_2$ and,
$\Omega_2^o = c_3$
$c_2$ can be taken in union with any of the sets since its addition does not affect the minimization problem. According to our decision $D(\Omega_1^o, \Omega_2^o)$ if $x \in c_1 \cup c_2$ $\Longrightarrow x \in \omega_1$. Using some basic rules of conditional probability -
$ P(\omega_1|x) = \dfrac{P(\omega_1)p(x|\omega_1)}{p(x)}$
$P(\omega_2|x) = \dfrac{P(\omega_2)p(x|\omega_2)}{p(x)} $
where $P(\omega_1|x)$ and $P(\omega_2|x)$ are known as posterior probabilities. $p(x)$ acts as the normalization factor in both the fractions. Which brings us to the usual text book version of Bayes’ rule that -
$x \in \omega_1$ if $ P(\omega_1|x) > P(\omega_2|x)$
$x \in \omega_2$ if $P(\omega_2|x) > P(\omega_1|x)$
To reach to this decision rule we didn’t impose any conditions on the sample space or take any assumptions. Thus no other partitioning can yield a smaller probability of error.
If Bayes’ rule is as good as we claim, why don’t we solve every classification problem by this rule? The answer lies in the details. Usually a classification problem consists of a training set and its associated labels. If we have $n$ samples then $\{X_i, y_i\}_{i=1}^{n}$ constitutes the training set where $X _i\in \Re^d$ and $y_i \in \Re$. We can easily calculate the prior probabilities of each class but usually the conditional densities $p(X|\omega_i)$ are not known. There is a huge amount of literature which deals with density estimation and making assumptions about class conditionals but that is beyond our scope. It can also become very difficult to calculate errors if the number of features increase since we need to calculate error integrals over complicated d-dimensional domains to estimate the efficiency of our estimator.
If someone wants to dwell into more details, similar arguments are presented in an excellent book on pattern recognition by Fukunaga. There’s also another blog post by Brandon Rohrer which deals with more practical aspects of Bayesian inference.